TOPOLOGICAL SEMANTICS: FOUNDATIONS OF THE DESCRIPTION OF THE SPATIAL DISTRIBUTION OF PROPOSITIONAL SIGNS

Introduction

The representation by the sentence the material properties of the world is recognized by L. Wittgenshtein as the main linguistic product of society interaction with the environment which is based on the rules of use of language and comparable linguistic technology [8]. Actually, the language itself in recent decades is interpreted as a technology [13, 16, 23]. Technological status of languages due to the fact that symbolic systems must correspond to the new communicative needs of the person and to meet the requirement of accessibility in the use. The degree of language technological effectiveness is its suitability in the process of adjusting the language of personality and informational transformations of the life-context can be tested empirically by connective technologies [9].

The world, according to the concept of L. Wittgenshtein [1] is set of numerous facts, the totality of which is defined as everything that occurs and everything that don’t has. The sentence is the sign which modeling and representing the world of facts, or actual world. "The sign through which we Express the thought I call the propositional sign (Satzzeichen). And the sentence is a propositional sign in its projective relation to the world" [1, P. 52]. The essence of a propositional sign is that its elements, words, incorporate it in a certain way that allows us to recognize the propositional sign as a fact. Importantly, the idea in the sentence for L. Wittgenstein expressed sensually: the sensible signs are used as projections of the possible state of affairs. Projection method is defined as thinking of the sentence meaning, in the same sentence does not contain its sense, but only the possibility of its expression, the form of its meaning, but not its contents.

Method: The topological representation of facts and signs in logical and semantic spaces

The scale of reality is defined by representation of facts in logical space, in which the position of the sign is determined by the mark relative to its surroundings or to near stay signs. In this case the sign is a standalone form or part of the form and relative semantic continuum – the set of concepts with which the sign can be associated. It is "clot" of contents or the marker sequence of meanings.

As for the location of the sign in a logical, semantic spaces and space of forms, then for its interpretation it is advisable to involve topological ideas and related logical ideas. M. McMullen [20] as the most relevant topological perspective, first defines the transformation of the shape associated with a metric space and a specific distance between the points. Important is the transformation of three-dimensional form in the plane form, that is also relevant to studies of the events shape transformations, events semantics and environment in a text-mode transmission, i.e., location in a particular system of propositional signs, which correlated with a specific conceptual set. Topological spaces form the broadest regime, in which matter the concept of ‘continuous function’.

R. Parikh, L. S. Moss, K. Steinsvold [24] believe that a large part of topology can be considered as a modal logic, i.e. epistemic logic which combines the notion of knowledge and effort. The researchers examine the ratio of logic and space, or rather, they pay attention to how different goals will dictate the formulation/selection logic. But in a sense, the goal is to, based on a common mathematical model of space, to select logical methods to work with this space.

In his work R. Parikh, L. S. Moss, K. Steinsvold rely on the understanding of the topology suggested by Stephen Vickers: “topology is used to explain approximate states of information: the points include both approximate points and more refined points, and these relate to the topology by the property that if an open set contains an approximate point, then it must contain any refinement of it.” [33, P. 3]. Finite observations become object of consideration therefore the main task of topology reconstruction in terms of logics of observations. The algebraization of a logic of finite observations is called a frame and the operation ∧ (binary) and (infinitary). The concept of the frame determines the emergence of a more topological notion of ‘a locale’, which is based on the frame morphisms into a special two-element frame. The semantics begins with a frame, a set whose elements are called worlds or points together with a binary relation on it. This relation is sometimes called accessibility, and symbols like →, ≤, or R have been used for it.

Discussion: The parthood semantics as the topological perspective on the logical  relationship 'part' to'whole'

A O. Prosorov [26] proposes to consider as varieties of formal textual syntax systematic interpretation of logical notions in terms of topology and order, drawing attention to the fact that for the word συґνταξιζ is derived from συґν (together) and ταґξιζ (order). In addition, the Prosorov O. A introduces the concept of semantic topology on texts, which is based on a topological interpretation of the core hermeneutic idea - the ratio of ‘part’ of text to ‘whole’ text [25, 26, 27]. The topological perspective on the relationship 'part' to'whole' allows you to enter the interpretations of the topological concepts, e.g., concepts of boundaries and interiors of objects. The topological perspective to consider cognitive important part of the whole, the lexical objectification parthood semantics declared by the opposition "single-multiplicity" [10, 12, 22, 21].

The study of the parthood semantics is part of mereology, which allows us to identify the deeper aspects of the ratio of ‘part’ to ‘whole’, but also to give new interpretations of concepts such as sum or fusion, and collection [17, 18, 31, 32, 11, 5, 2].

‘Part’ of the text, interpreted O. Prozorov as subsequence which graph is a subset of the whole sequence graph. The text is understood as a finite sequence of its constituent sentences and so it is formally identified with a graph of the function. Understanding the semantic content of the text related to the meaningful parts and the meanings of these parts determine the meaning of the whole. According to O. Prozorov, to understand a meaningful part U of the text is to understand contextually all its sentences x ∈ U. While the context of a particular sentence x истолковывается как some meaningful part lying in U. For the least meaningful part Ux containing x, we have that x ∈ U ∩ V implies x ∈ Ux ⊆ U ∩ V ; hence, U ∩ V is meaningful as a union ∪x∈U∩V Ux of meaningful parts.

In accordance with the concept of topological semantics O. Prozorov, it is assumed that any text has a value as a whole, it only remains to determine formally its empty part (for example, as a singleton) in order to provide it with some topology in the mathematical sense, where the collection of open sets 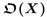  whose boundaries are set as the set of all meaningful parts.

Results: Topological schema as the unit of calculation of the topological semantics and spatial values

E. V. Rahilina [6] finds that every object in the language picture of the world corresponds to a specific topological type – a functionally important class of shapes, which include surfaces, containers, etc. In addition, the researcher [7] suggested to call an image schema as topological schema. Image schema was introduced into science by M. Johnson "An image schema is a recurring, dynamic pattern of our perceptual interactions and motor programs that gives coherence and structure to our experience" [15].

V. Evans and M. Green [14, P. 190], synthesizing different points of view on images schemas and integrating generated by the authors of the lists that offer a list of topological models, which is as follows: SPACE: up–down, front–back, left–right, near–far, centre–periphery; CONTAINMENT: contact, straight, verticality, container, in–out, surfaсe, full–empty, content; LOCOMOTION: momentum, source–path–goal; BALANCE: twin–pan balance, локальное, point balance, equilibrium; FORCE: compulsion, blockage, counterforce, diversion, removal of restraint, enablement, attraction, resistance; UNITY–MULTIPLICITY: merging, collection, splitting, iteration, part–whole, mass–count, link(age); IDENTITY: matching, superimposition; EXISTENCE: removal, bounded space, cycle, object, process.

N. Kuznetsov [3] in the context of spatial values of local cases of Komi language recognizes the most important topological schemas container, surfaсe, source–path–goal, etc. The intra local cases in their basic spatial functions are an indication of internal localization, however, depending on the topological type of the landmark and its physical characteristics, they can also be used to specify other locations. Under the spatial functions of the cases is understood the designation of their physical position, action or motion of the trajector relative to a spatial reference point.

Situation use of the intra local cases in the basic values are similar, they denote the same location and involve the same types of topological landmarks. However, they differ in the designation of types of topological orientation: specify the location of the trajector, marking the final point of motion or action, the expression of the starting point.

Conclusion

A. Sharif, M. Egenhofer, D. Mark [30] notice that the spatial relations reflect the ways in which people perceive the spatial configuration and describe them in different languages. Analyzing the works devoted to spatial relations [29, 34], researchers have come to the conclusion that there are three basic types of spatial relations: 1) topological relationships based on the notion of neighborhood and invariant under consistent topological transformations, such as rotation, translation, scaling; 2) cardinal direction relations, which are based on the existence of a vector space and is subject to change under rotation, while they are invariants under translation and scaling of the reference frame; 3) distance relations express spatial properties that reflect the concept of a metric and, therefore, changes in the calculation, but are invariant under translation and rotation.

D. Mark, M. Egenhofer [19] note that the semantics of spatial relations multidimensional that affects the choice of words users of the language. It is the values of the objects, shape of objects and their scale, relationships in space between objects. The level of culture affects the choice of words, education and the quality of the natural language of the individuals that use spatial terms.

The use of mathematical concepts in the analysis of the properties of the artistic space of the 80-ies of XX century in the context of spatial semiotics proposed Y. M. Lotman [4]. The space is understood as the totality of homogeneous objects (phenomena, conditions, facts, figures, values of variables, etc.) between which there are relationships similar to ordinary spatial relationships. Applied to artistic works mathematical concepts of space is a modeling language, which can be any values as long as they. have the character of structural relations [4, P. 4].