Числительные в текстах как характерная особенность авторского стиля
Числительные в текстах как характерная особенность авторского стиля
Аннотация
Рассмотрено применение нового количественного метода изучения авторского стиля литературных текстов. Метод основан на компьютерном анализе статистики числительных, встречающихся в текстах. Показано, что количественные и порядковые числительные, используемые автором в (художественном) тексте, индивидуальны для каждого автора; их совокупность является характерным признаком, различающим тексты разных авторов. Выполнен сопоставительный анализ литературных текстов И.А. Бунина и А.И. Куприна; для проверки методологии дополнительно исследованы произведения Ф.К. Сологуба, М.П. Арцыбашева. Результаты анализа подвергнуты иерархической кластеризации, правильно разделившей тексты в соответствии с авторством и жанром.
1. Введение
Задачи стилометрии, к которым относится количественное изучение авторских особенностей текстов (в т.ч. для их атрибуции) до настоящего времени не имеют вполне удовлетворительного решения , : традиционно вычисляются частоты встречаемости в текстах знаменательных частей речи и служебных слов (предлоги, союзы), средние длины слов и предложений; в паре анализируемых текстов сравниваются самые часто встречающиеся слова и даже буквосочетания (как ни странно, последний подход часто даёт неплохие результаты). К сожалению, разные методы часто приводят к несогласующимся выводам.
Хорошие результаты получены с помощью нейронных сетей , а вскоре, по-видимому, искусственный интеллект сможет успешно решать задачи стилометрии, но содержательная интерпретация результатов при этом затруднительна, поскольку метод, опирающийся на применение нейронных сетей, является «чёрным ящиком».
Нами разработан оригинальный подход к анализу авторских (литературных) текстов, основанный на учёте использования авторами числительных в их текстах , . Такой подход имеет немалые преимущества. Среди знаменательных частей речи числительные по своей природе наиболее легко поддаются количественному учёту. Кроме того, среди всех особенностей текста, анализируемых в стилометрии, пожалуй, только встречаемость числительных практически не меняется при переводе текста на другой язык (за малозначимым вычетом числительных, входящих в идиомы – см. ниже). Это расширяет возможности текстологического анализа, позволяя, например, в случае необходимости привлекать тексты, имеющиеся на языке-посреднике.
Применительно к художественному тексту, содержание которого не является жёстко привязанным к реальным событиям, а порождено свободным воображением, естественно предположить, что употребление числительных связано с психологическими особенностями автора, неосознанно для него самого влияющими на результат творчества (в рамках выбранных жанра, сюжета и т.п.). Следовательно, манера использования числительных – это авторская особенность (fingerprint), позволяющая при определённых обстоятельствах решить проблему авторства текста.
Наше предположение подтвердилось; анализ произведений нескольких десятков авторов на русском, чешском, английском языках обнаружил ощутимые авторские особенности употребления числительных в текстах, влияние на них жанра, стиля, художественного направления , , , . В частности, недавно нами решена важная проблема чешского литературоведения, связанная с авторством некоторых текстов, приписываемых классику чешской литературы – Петру Безручу . Таким образом, результаты анализа встречаемости числительных допускают содержательное филологическое истолкование.
В данной работе мы проанализируем основные литературные произведения И.А. Бунина (1870–1953) и А.И. Куприна (1870–1938) с точки зрения использования числительных. Литературная критика часто рассматривает эти имена совместно, а в художественной манере Нобелевского лауреата по литературе Бунина и его современника Куприна, которого Бунин высоко ценил, находят немало общего , , . До сих пор сопоставление ограничивалось традиционными филологическими подходами.
В современной стилометрии укоренилось мнение, что даже при сопоставлении текстов двух авторов доказательную силу об их сходстве будет иметь лишь анализ, в котором изучаемые тексты «разбавлены» множеством посторонних текстов других авторов (т.н. impostors) . Следуя этим идеям, мы ввели в рассмотрение произведения двух современников Бунина и Куприна – Ф.К. Сологуба (1863–1927) и М.П. Арцыбашева (1878–1927). Выбор диктовался частичным совпадением художественных направлений всех четырёх литераторов , , и личными предпочтениями автора настоящего исследования.
2. Метод и объекты исследования
Нами разработана компьютерная программа, отыскивающая в русскоязычном тексте количественные и порядковые числительные, выраженные как цифрами (числа), так и словесно в разных словоформах. Поиск основан на сличении слов текста со словарной базой из словаря: «М. Хаген – Полная парадигма. Морфология. Частотный словарь. Совмещенный словарь» (http://speakrus.ru/dict2/#morph-paradigm).
Предварительно из текста автоматически удалялись идиоматические выражения и устойчивые фразы, случайно содержащие числительные («семь пятниц на неделе», «ясно как дважды два четыре» и т.п.); вручную удалялись числительные, не связанные с авторским художественным замыслом – номера страниц, глав, перечисления 1), 2), 3), … и т.п.
Мы проанализировали наиболее объёмные произведения Бунина, Куприна, Сологуба и Арцыбашева, представленные в табл. 1.
Таблица 1 - Встречаемость числительных в исследованных произведениях
№ | Автор, текст, год создания | Объём (байты, кодировка UTF) | Количество числительных | Обратная плотность числительных |
1 | Бунин, Жизнь Арсеньева (1929) | 987966 | 588 | 1680,2 |
2 | Бунин, Стихотворения | 921097 | 322 | 2860,5 |
3 | Бунин, Темные аллеи (опубл. 1943) | 796064 | 548 | 1452,7 |
4 | Бунин, Под серпом и молотом (опубл. 1950) | 756078 | 944 | 800,9 |
5 | Бунин, Деревня (1910) | 413138 | 272 | 1518,9 |
6 | Бунин, Окаянные дни (1920) | 408271 | 488 | 836,6 |
7 | Куприн, Яма (1915) | 1071674 | 1062 | 1009,1 |
8 | Куприн, Юнкера (1932) | 837555 | 992 | 844,3 |
9 | Куприн, Поединок (1905) | 795748 | 730 | 1090,1 |
10 | Куприн, Лазурные берега (1913) | 312916 | 492 | 636,0 |
11 | Куприн, Киевские типы (1897) | 166941 | 169 | 987,8 |
12 | Сологуб, Стихотворения | 1037506 | 357 | 2906,2 |
13 | Сологуб, Мелкий бес (1902) | 887247 | 393 | 2257,6 |
14 | Арцыбашев, У последней черты (1912) | 1566573 | 774 | 2024,0 |
15 | Арцыбашев, Санин (1907) | 1045996 | 427 | 2449,6 |
16 | Арцыбашев, Женщина, стоящая посреди (1915) | 409174 | 178 | 2298,7 |
17 | Арцыбашев, Смерть Ланде (1904) | 376880 | 149 | 2529,4 |
3. Основные результаты
Для каждого произведения найдена обратная плотность числительных как результат деления объёма текста на количество найденных в нём числительных. Чем меньше обратная плотность, тем чаще в тексте встречаются числительные.
В связи с этим понятны сравнительно малые значения обратной плотности в мемуарном (№4), дневниковом (№6) и очерковых (№10, 11) текстах, в которых неизбежно обилие фактографических числовых подробностей.
Сравнение обратных плотностей числительных для художественных текстов обнаруживает существенное различие между произведениями Бунина (№1, 3, 5) и Куприна (№7, 8, 9): в текстах последнего числительные используются чаще (детализация больше).
Наконец, обратим внимание на большие обратные плотности для поэзии (№2, 12), которой, вообще говоря, не свойственна детализация.
Проза Сологуба и Арцыбашева, добавленных в качестве impostors (№13–17), отличается очень большими значениями обратной плотности, статистически достоверно отличными от значений для прозы Бунина и Куприна.
Эти результаты показывают, что использование числительных специфично для автора и жанра.
В табл. 2 представлены абсолютные частоты числительных 1, 2, …, 5, которые содержатся во всех исследованных произведениях. Поскольку тексты сильно различаются по размеру (см. табл. 1), для сравнимости абсолютных частот числительных в разных текстах мы ввели поправочные коэффициенты, выбрав в качестве эталонного текста для сравнения «Яму» Куприна. Поэтому, например, частоты числительных в «Жизни Арсеньева» Бунина пришлось умножить на 1071674/987966 = 1,08, а для романа «У последней черты» Арцыбашева – на 1071674/1566573 = 0,68.
Абсолютные частоты числительных с поправкой на размер текста приведены в скобках в табл. 2.
Таблица 2 - Абсолютные частоты числительных 1, 2, …, 5 в исследованных текстах и исправленные абсолютные частоты (в скобках) с поправками, учитывающими разный размер текстов
№ | Автор, текст | числительные | ||||
1 | 2 | 3 | 4 | 5 | ||
1 | Бунин, Жизнь Арсеньева | 355 (385,1) | 101 (109,6) | 50 (54,2) | 4 (4,3) | 10 (10,9) |
2 | Бунин, Стихотворения | 152 (176,9) | 56 (65,2) | 19 (22,1) | 15 (17, 5) | 6 (7,0) |
3 | Бунин, Темные аллеи | 248 (333,9) | 99 (133,3) | 46 (61,9) | 13 (17,5) | 20 (26,9) |
4 | Бунин, Под серпом и молотом | 306 (433,7) | 99 (140,3) | 48 (68,0) | 14 (19,8) | 18 (25,5) |
5 | Бунин, Деревня | 105 (272,4) | 46 (119,3) | 31 (80,4) | 7 (18,2) | 13 (33,7) |
6 | Бунин, Окаянные дни | 140 (367,5) | 53 (139,1) | 30 (78,8) | 10 (26,3) | 9 (23,6) |
7 | Куприн, Яма | 392 (392) | 172 (172) | 101 (101) | 34 (34) | 47 (47) |
8 | Куприн, Юнкера | 313 (400,5) | 208 (266,1) | 112 (143,3) | 80 (102,4) | 27 (34,6) |
9 | Куприн, Поединок | 302 (406,7) | 127 (171,0) | 66 (88,9) | 25 (33,7) | 38 (51,2) |
10 | Куприн, Лазурные берега | 140 (479,5) | 88 (301,4) | 54 (184,9) | 25 (85,6) | 26 (89,0) |
11 | Куприн, Киевские типы | 59 (378,8) | 26 (166,9) | 22 (141,2) | 11 (70,6) | 6 (38,5) |
12 | Сологуб, Стихотворения | 209 (215,9) | 72 (74,4) | 25 (25,8) | 12 (12,4) | 3 (3,1) |
13 | Сологуб, Мелкий бес | 176 (212,6) | 79 (95,4) | 50 (60,4) | 15 (18,1) | 12 (14,5) |
14 | Арцыбашев, У последней черты | 496 (339,3) | 105 (71,8) | 46 (31,5) | 9 (6,2) | 7 (4,8) |
15 | Арцыбашев, Санин | 283 (290,0) | 72 (73,8) | 22 (22,5) | 1 (1,0) | 3 (3,1) |
16 | Арцыбашев, Женщина, стоящая посреди | 122 (319,5) | 30 (78,6) | 10 (26,2) | 5 (13,1) | 2 (5,2) |
17 | Арцыбашев, Смерть Ланде | 106 (301,4) | 22 (62,6) | 4 (11,4) | 2 (5,7) | 3 (8,5) |
Ещё более определённые результаты, чем при анализе обратных плотностей числительных, были получены при использовании иерархического кластерного анализа, объединяющего объекты в кластеры по принципу сходства. Как известно, мерой его является метрика ρ («расстояние»): чем меньше «расстояние» между объектами, тем больше сходство между ними. Мы применили манхэттенскую метрику
где x и y – n-мерные векторы, компонентами которых являются исправленные абсолютные частоты (см. табл. 2) первых n натуральных чисел в двух анализируемых текстах (здесь n = 5, т. к. во всех исследованных текстах встречались числительные от одного до пяти).
В процессе кластеризации использован метод дальнего соседа, который приводит к образованию компактных, чётко очерченных кластеров , .
Как известно, выбор метрики и метода кластеризации невозможно строго обосновать; между тем, они способны существенно повлиять на результаты кластеризации. В нашем случае результаты оказались достаточно устойчивыми; другие разумные комбинации метрики и метода кластеризации лишь несущественно влияли на вид дендрограммы (рис. 1).
Исследованные тексты практически идеально распределились по кластерам в соответствии с авторством и жанром.
Использование числительных в текстах Бунина более единообразно, чем у Куприна: все прозаические тексты попадают в родственные кластеры с небольшой высотой слияния. Единственный файл, попавший в другой кластер – это стихи Бунина, которые вполне логично кластеризовались вместе с поэзией Сологуба.
Наблюдается некоторая временнáя эволюция использования числительных: произведения, близкие по времени создания, чаще попадают в один или родственные кластеры.
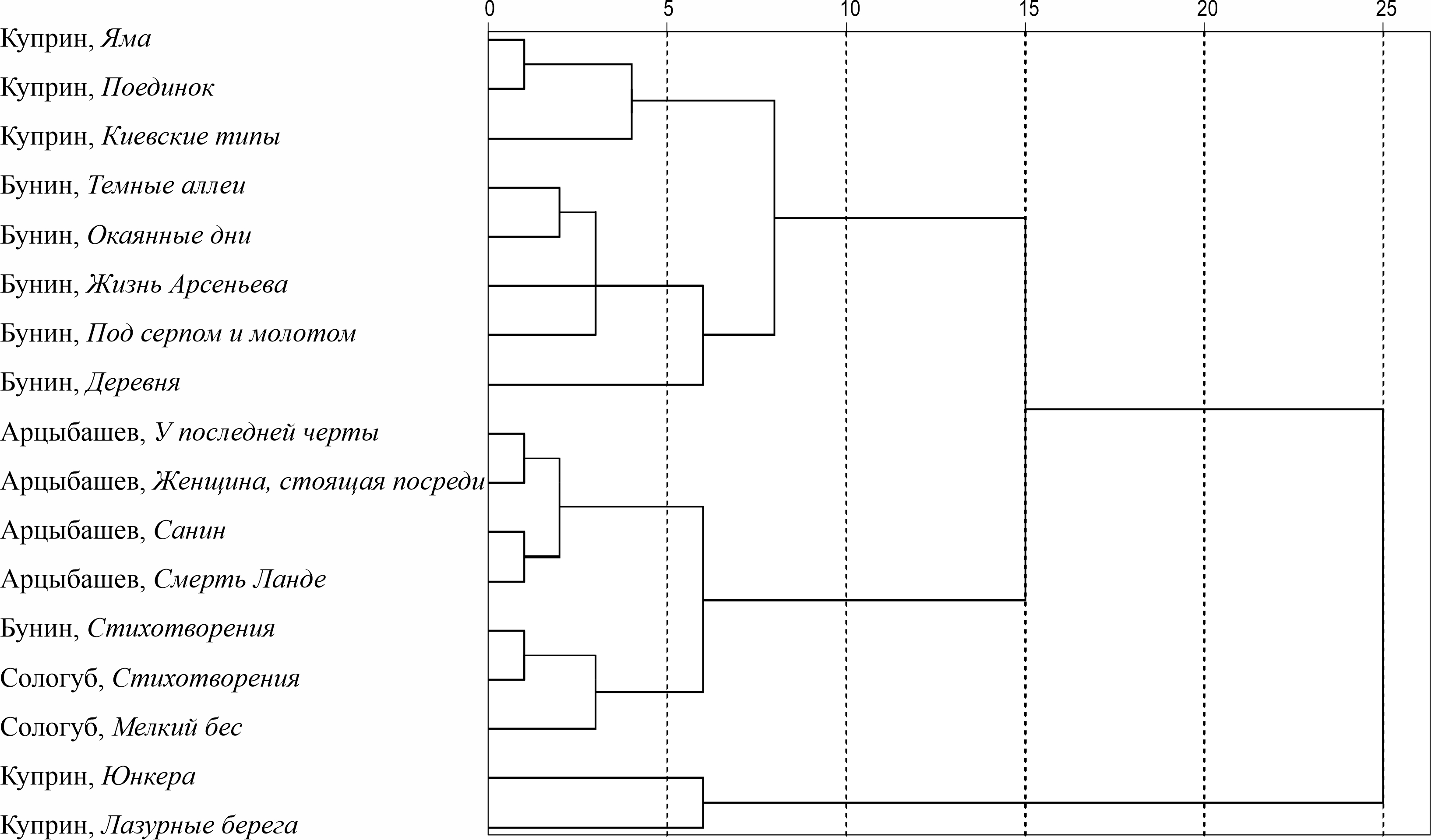
Рисунок 1 - Результат применения иерархического кластерного анализа к литературным текстам И.А. Бунина, А.И. Куприна, Ф.К. Сологуба и М.П. Арцыбашева. По вертикальной оси отложено «расстояние» в произвольных единицах
4. Заключение
Разрабатываемый нами новый подход к задачам стилометрии, основанный на анализе статистики числительных в текстах, при всей его простоте, демонстрирует высокую эффективность и чувствительность. Показано, что манера использования числительных индивидуальна у каждого автора; их совокупность является характерным признаком, различающим тексты разных авторов. Тексты И.А. Бунина и А.И. Куприна, сравнительный анализ которых выполнялся до сих пор лишь в рамках традиционного описательного филологического подхода, впервые подвергнуты формальному количественному анализу, правильно распределившему тексты согласно авторству и жанрам. Использование числительных в текстах Бунина оказалось более единообразным, чем у Куприна. Привлечение для анализа текстов сторонних авторов (impostors) – Ф.К. Сологуба и М.П. Арцыбашева – усиливает значимость полученного результата и подтверждает его неслучайный характер.
